1. One-Minute Refresher
In a previous article, I argued for Doug’s Law as a way of understanding Mary’s room without rejecting physicalism:
I used the example of an alien language, Myosian, which we didn’t know and had almost no underlying similarity to English. There are ways you could learn to interpret Myosian—by having an English translation, by having objects pointed out with their corresponding Myosian script, by having a superintelligence who understood both languages tutor us. But if your only instruction in how to read Myosian is written in Myosian, you will never be able to interpret the text, even if the Myosian description in principle represents all the facts you need to know to understand the Myosian language. I then coined the term “Doug’s Law,” named for Douglas Hofstadter:
Doug’s Law: how to interpret a language cannot be communicated in that language alone.
Like I said, I’m not the first to try to apply this argument to Mary’s Room. But I’d like to bring what (I believe to be) a new layer of computational rigor to the analogy. I’d like to argue that if you think minds operate like computers, then you shouldn’t be terribly surprised in there being wholly physical properties which no amount of instruction can teach you to compute. Again, I try to present a version of events that is compatible with physicalism to defend against strong claims like “Mary’s Room Refutes Physicalism,” even if physicalism is not the best explanation for what’s going on here.
2. P-strings and DFAs
A parentheses-string, or p-string, is a finite sequence of the symbols ( and ). The following are all p-strings:
())))))))((((()))())())((((()(
P-strings can have many properties, such as:
Having only
(symbolsBeing 10 symbols long
Including at least two
()()()sequencesSpelling out an English word in ASCII binary, where
(= 0,)= 1 [for instance,())()(((())()(()(((()()(spells out “hi”.]
Each property listed above is either true or false of any given p-string, never indeterminate. Let’s call properties of this type boolean properties. Define a p-string boolean computer to be an algorithm that accepts a p-string as input and prints out either true or false as output. A p-string boolean computer computes a boolean property X just in case for any p-string inputs S, the computer prints true iff S has property X.
One type of boolean computer is called a deterministic finite automaton, or DFA. A DFA reads a p-string one symbol at a time from left to right. It has a finite set of states, some of which are accept states and the rest of which are reject states. It begins on its start state, which can either be an accept or a reject state. Each time a DFA reads a symbol, it consults its transition function which tells it, based on the current symbol and the current state, which state to go to next. Once the DFA has read the entire string, if it ends in an accept state it prints out true and if it ends in a reject state it prints out false. Here’s a flowchart for a DFA that computes the property of not having any ) symbols:
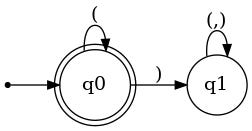
) leads you to a reject state, q1, from which there is no escape, but encountering only ( will keep you in q0. Generated by Gemini 2.5 Pro using the automata-lib library for Python.This DFA is rather simple, but they can get more complex! Here’s one that computes the property of including at least two ()()() sequences:

I won’t try to draw the DFA that computes the property of spelling out an English word in ASCII binary, but I can fully conceptualize how it would work. You can build a DFA that would decode the first 8 symbols (since each ASCII symbol is 8 bits) and end in one of 27 states, each one corresponding to a letter of the alphabet plus one for “gibberish” that would be rejected [((((((((, for instance, would correspond to the ASCII null byte, which is not an English letter.] Then you could tack on a duplicate of the first DFA’s flowchart to each of those non-gibberish end states, ending in 26² non-gibberish end states, representing the first two letters of the word, and so on. The longest English word is still finite length, so you can stop after that many characters or once the symbol is done. Then make each end state that corresponds to a complete English word an accept state, and all the rest reject states. It would be monstrously complicated, but a big enough DFA is in principle capable of handling it.
You can even feed instructions on which property to compute to a DFA, to a certain extent! Here’s how that would work:
Suppose DFA A and DFA B compute p-string properties X and Y respectively.
Let DFA C contain a copy of DFA A and a copy of DFA B, plus a single additional reject state which becomes the start state of DFA C.
From this start state, if DFA C reads a
(it transitions to the first state of DFA A. Otherwise, it transitions to the first state of DFA B.Therefore, given a p-string S, DFA C will compute property A for S given the input
(S and compute property B given the input)S.1
DFAs, in short, can compute a wide range of properties, and even have a certain ability to take in instructions as to which properties to compute. But there are some limits that no amount of flowchart cleverness can overcome.
3. The Matchingness Property
As any English teacher or software dev will tell you, parentheses should come in pairs. A p-string is matching iff every ( has a unique corresponding ) later in the string and every ) has a unique corresponding ( earlier in the string. For instance:
(): matching(((): not matching(()(()())): matching)))))(((((: not matching
Matchingness is a boolean property: every p-string is either matching or not matching. And it’s a pretty simple one, too: I could write a boolean computer for matchingness in a few lines of Python.
But a DFA can’t handle it. DFAs are provably incapable of computing matchingness over the set of all p-strings. No matter how many states it has, no matter what schemes you cook up for instruction prefixes, no matter what facts in what clever encoding you present to the DFA, it can’t compute matchingness.
To be sure, DFAs can compute lots of properties that are associated with matchingness. A DFA could reject some classes of p-strings that are all non-matching: those that only contain one type of symbol, or that end with a ( or start with a ), and so on. It could compute some stricter, simpler property that is sufficient but not necessary for matchingness, such having the form (), ()(), ()()(), … . But no DFA can compute matchingness itself.
It’s obvious to us that matchingness isn’t some kind of weird, ghostly, or contingent property. Matchingness or lack thereof is entailed by the sequence of symbols that makes up a p-string, and a p-string just consists of those symbols in that order. It is not possible that the p-string (()()) is matching in this world but that there could be a physically identical p-string in a another world which lacks matchingness. In short, there are no “zombie” p-strings.
But this fact isn’t obvious from the epistemic vantage point of the DFAs. If your brain only had the computational sophistication of a DFA, then you would be unable to grasp what matchingness really is and how it could possibly be entailed by the structure of a p-string. You would be able to recognize things associated with matchingness, but even an extensive definition of the word matchingness would be totally beyond you. Your mind would be too limited to think in terms of possibility and impossibility, but a zombie p-string would be perfectly compatible with your knowledge.
4. The Mary Analogy
In Mary’s room, a human is presented with all the physical facts about red, encoded in English science textbooks or black-and-white TV. From engaging with these resources, she can learn many facts about redness. For instance, from the sequence of Latin-alphabet symbols red has a dominant wavelength of approximately 625–750 nanometers, and from her background knowledge of what words like “wavelength”, “approximately”, and “nanometers” mean, she is able to learn the fact that red has a dominant wavelength of approximately 625-750 nanometers.2
Many physicalists believe the mind is, or is like, a physical computer. Let’s call this view computationalism.
If computationalism is true, then the process of how Mary comes to know facts by looking at strings of symbols or black-and-white pixels on a grid is a computational process, run by on a physical computer (the brain).
We know that some theoretical computers, like DFAs, cannot compute certain properties of their inputs, even if they are presented with all of the basic facts that logically entail that property, in an arbitrary encoding.
Since physical computers are more limited than theoretical computers (having to deal with memory, heat, lag time, etc.), it follows that some physical computers cannot compute certain properties of their inputs even if they are presented with all the physical facts that logically entail that property, in an arbitrary encoding.
The anti-physicalist tells us that Mary, when presented with all the physical facts about red in a particular encoding (English text and black-and-white television), can learn a whole slew of properties of red but cannot learn properties like what it is like to see red.
However, this is compatible with computationalism even if the computationalist believes “what it is like to see red” is a physical fact. It is compatible because of #3—Mary’s mind is a computer, and some computers have limits in what properties they can compute even if they have all the relevant facts in front of them.
Therefore, Mary’s room does not refute computationalism.
Perhaps this idea of massive computational limits on the human brain seems farfetched. But we can readily accept that if Mary had less than normal-human computational capability, she would not be able to learn plenty of facts even if presented with the same knowledge. If Mary were placed in this room as a baby, with no human contact, she would never learn what those funny squiggles on the paper meant, even if the textbook gave full instructions on how to read English. Using those instructions would require already being able to interpret English text, thus making them useless. This is Doug’s Law and the main argument of the previous post. Similarly, if Mary had a severe neurological syndrome, such as anterograde amnesia, she would be able to understand each individual sentence’s meaning but would quickly hit a cap of how much she could understand before forgetting basic facts needed for understanding more complex ones.
So why should we believe that the current neurotypical level of human computational capability, the kind Mary presumably has, is sufficient to learn all physical facts about the universe from textbooks and black-and-white video? We would not accept the inability of a baby to learn quantum physics from comprehensive research articles as evidence that that there are facts about quantum physics that cannot be described by research articles. Why should we think any differently about Mary?
5. Objections
A smart anti-physicalist will answer that computationalists still have to account for the fact that Mary, unlike a DFA or a baby on their respective tasks, can learn facts like what it is like to see red, once she actually sees red. Under computationalism, that’s also a computation run by the brain, so it is not the case that a brain is in principle incapable of computing the property of “redness” from physical information. Why should she be able to compute redness from information presented as light waves hitting her eyes and not from different light waves hitting her eyes that let her read a textbook?
Simple: the brain has many parts, at varying degrees of sophistication. Monkeys can see red,3 but they can’t understand many physical facts about them, even though a monkey brain and a human brain are both made of the same basic parts (neurons, glial cells, neurotransmitters, etc.). Some humans with damage to their primary visual cortex report blindness yet can process visual information subconsciously, suggesting that the capabilities of conscious, reflective visual processing aren’t the same as the whole toolkit the brain has to offer.4 And, as in the case of anterograde amnesia, damage to one part of the brain can ruin slow, intensive processes of learning like reading from textbooks while leaving immediate pathways (like looking at colored objects) intact. Knowing this, it isn’t that crazy to me that our visual cortex might be able to perform computations that our deliberative, rational brain areas can’t.
Others might object that there’s some sleight of hand going on with the term “physical” here. What defines a physical fact, other than that it can be communicated in the laws of physics, chemistry, biology, etc.? This objector might simply define physical facts as the sum of all facts that can be communicated in a completed science. If this is what you mean by physical, then you may be justified in saying that what it is like to see redness is not one of those facts—at the very least, this article does not challenge that perspective.
But this article does challenge the link between “redness is not communicable to other humans through writing about physics” to “redness is metaphysically contingent” or “there could be zombie worlds that are physically identical to ours but in which no one experiences redness”. Just as the sequence of symbols of a p-string entails its matchingness, even if a DFA cannot recognize that fact, so too it might be that the facts we can capture in writing about physics entail what redness is like, even if we cannot recognize that fact. It is for that reason that my preferred definition of physical facts include not just the facts of a completed physics but also, at the very least, logically entailed by those facts: it avoids this confusion of modality.
6. Conclusion
Arguments by analogy aren’t as desirable as rigorous proofs, but if my view on Mary’s room is correct then I must necessarily argue by analogy, since part of my core conclusion is that we are incapable of fully understanding redness through linguistic communication. (You might as well try to argue with a DFA, a Myosian, or a baby.) I think DFAs and other analogies to language and computation can provide good intuition for how it could be that “what it is like to see red” be a physical fact and still be unlearnable by Mary.
I’m slightly abusing my definition of computing a property here, as DFA C does not print true iff )S has property X, but rather iff S has property X. A more rigorous definition of computation would say that a DFA computes property P given instruction prefix I iff, for any p-string S, the DFA prints true on input IS iff S has property P. Under this definition, DFA C computes property X given instruction prefix ( and computes property Y given instruction prefix ).
“Red.” In Wikipedia, May 10, 2025. https://en.wikipedia.org/w/index.php?title=Red&oldid=1289671297.
Dominy, Nathaniel J., and Peter W. Lucas. “Ecological Importance of Trichromatic Vision to Primates.” Nature 410, no. 6826 (March 2001): 363–66. https://doi.org/10.1038/35066567.
Leopold, David A. “Primary Visual Cortex: Awareness and Blindsight.” Annual Review of Neuroscience 35, no. Volume 35, 2012 (July 21, 2012): 91–109. https://doi.org/10.1146/annurev-neuro-062111-150356.




as someone who knew nothing abt p-strings or dfas, i found this interesting, definitely a solid expansion to the ideas you introduced in prior articles